Function
A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.

f(x)=anxn+an−1xn−1+…..+a1x1+a0 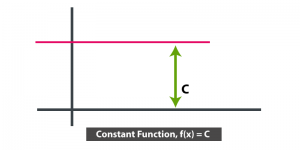


f(x)=5x3−2x2+3x+6 g(x)=3x+4√(x−1)2
A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.
Representation-
Cartesian product of 2 sets is mapping every element to every element of other set. It is generally represented as X
A={"a","b"}, B={"y","z"} then A X B= {("a","y"),("a","z"),(b,y),(b,z)}
Relation: A Relation R from a non-empty set A to a non empty set B is a subset of cartesian product A X B.
n(A)= number of element in set A.
n(B)= number of element in set B.
Let 's say n(A)=p, n(B)=q n(A X B)=pq then no of relations possible from A to B is 2^pq
A relation f from a set A to a set B is said to function if every element of set A has one and only one image in set B.
Relation: A function f is X to Y then f: X->Y X is called domain set, Y is called range function.
Functions are generally represented as f(x)
Let , f(x)=x3
It is said as f of x is equal to x cube.
Functions can also be represented by g(), t(),… etc.
Lets Work Out-
Example- Find the output of the function
(i) t = 0
(ii) t = 2
Solution- The given function is
(i) At t = 0,
= 5
(ii) At t = 2,
= 29
|
Types of Functions-
One-to-One function – It signifies that one element of a set is related to one element of the other set.

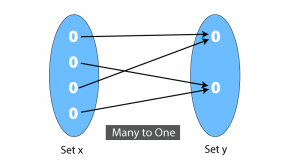
Many-to-One-function- It signifies that many elements of a set is related to one element of the other set.

Note :
One-to-Many- A function cannot have a one to many relation ie. one element of a set cannot be related to more than one element of the other set.
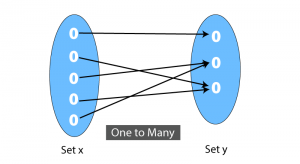 |
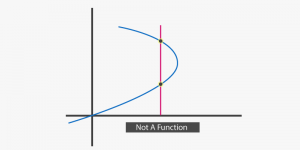
Vertical Line Test-
Vertical line test is used to determine whether a curve is a function or not.
If any curve cuts a vertical line at more than one points then the curve is not a function.

Types of Functions-
Polynomial function-
A polynomial function can be expressed as :
The highest power in the expression is known as the degree of the polynomial function. The different types of polynomial functions based on the degree are:
- The polynomial function is called as Constant function if the degree is zero.
- The polynomial function is called as Linear if the degree is one.
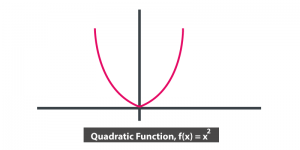
- The polynomial function is Quadratic if the degree is two.
- The polynomial function is Cubic if the degree is three.
Constant Polynomial Functions
The polynomial of 0th degree where f(x) = f(0) = a0

Linear Polynomial Functions
A linear polynomial function is a first degree polynomial where the input needs to be multiplied by m and added to c. It can be expressed by f(x) = mx + c.
For example, f(x) = 2x + 1 at x = 1
f(1) = 2.1 + 1 = 3
f(1) = 3

Quadratic Polynomial Functions
A Quadratic polynomial function is a second degree polynomial and it can be expressed as;
F(x) = ax 2 + bx + c, and a is not equal to zero.
Where a, b, c are constant and x is a variable.
Example, f(x) = 2x 2 + x – 1 at x = 2
If x = 2, f(2) = 2.2 2 + 2 – 1 = 9

Cubic Polynomial Function
A cubic polynomial function is a polynomial of degree three and can be expressed as;
F(x) = ax 3 + bx 2 + cx + d and a is not equal to zero.

Algebraic Functions
A function that consists of a finite number of terms involving powers and roots of independent variable x and fundamental operations such as addition, subtraction, multiplication, and division is known as an algebraic equation.
For Example-
Rational functions, irrational functions and Polynomials functions are examples of algebraic functions.
Comments
Post a Comment